Game of Life simulation

It's the Hello World v2.0 of software development - at some point in their career, everyone and their dog has written a simulation of Conway's Game of Life. The game simulates very simple cellular automata - given a cartesian grid of cells, each cell will either come to life, continue to live, or die for each iteration of the game, based on how many of its neighbours are alive. If a cell has 2 or 3 neighbours, it continues to live; if a cell has 3 neighbours, it comes to life, and otherwise, the cell dies.

I wasn't so much interested in a single game itself, but by the nature of the system across different board configurations - given a random starting board, how many iterations would it take for a board to die out completely?

Game Behaviour

For a 6x6 board, with a fill factor of ~30%, the histogram of board iterations looks like this after one million trials:

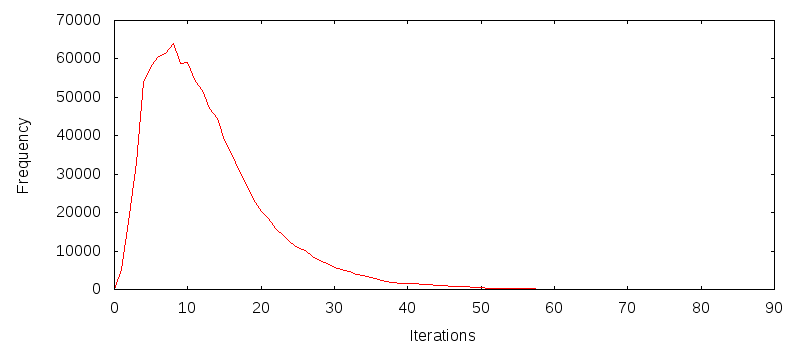
The iteration frequency appears to follow a log-normal distribution with a fair bit of skew, or a power log-normal distribution, and has peak of around 8 iterations; the error in this distribution is noto quite as visible with a smaller number of trials, but a small anomaly can be seen at iteration counts 8 and 9; it would appear that a larger number of boards stabilise within 8 rounds rather than 9, but I'm not entirely sure why at this stage.

Anyone interested in the raw data can grab the code themselves, or download the pre-baked 1 million iteration data.

Get the code

You can get a copy of the C++ code, released under the BSD license.

Contact Information

If you have any comments or queries, email me at gameoflife at this.domain.org.

License Information

This code is released under the BSD license, as per the header comments.